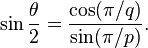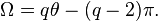جسم افلاطونی
 منبع:wikipedia
منبع:wikipedia
در هندسه اقلیدسی، یک جسم افلاطونی، یک چندوجهی منتظم و محدب با وجههایی بهصورت چندضلعی منتظم همنهشت است که تعداد یکسانی از وجهها در هر رأس با یکدیگر برخورد میکنند.
پنج جسم، این شرایط را احراز میکنند که هر یک با تعداد وجههایش نامیده میشود.
یک چندوجهی کوژ، جسم افلاطونی است، اگر و تنها اگر
- همهٔ وجههای آن چندضلعیهای منتظم همنهشت باشند.
- هیچکدام از وجههای آن با هم تلاقی نکنند، مگر در اضلاع آن.
- تعداد یکسانی از وجهها در هر یک از رأسها به هم برسند.
| Polyhedron | رأسها | ضلع | وجه | نماد شلفلی | آرایش رأسها | |
|---|---|---|---|---|---|---|
| چهاروجهی | ۴ | ۶ | ۴ | {۳, ۳} | ۳٫۳٫۳ | |
| مکعب |  | ۸ | ۱۲ | ۶ | {۴, ۳} | ۴٫۴٫۴ |
| هشتوجهی |  | ۶ | ۱۲ | ۸ | {۳, ۴} | ۳٫۳٫۳٫۳ |
| دوازدهوجهی |  | ۲۰ | ۳۰ | ۱۲ | {۵, ۳} | ۵٫۵٫۵ |
| بیستوجهی | ۱۲ | ۳۰ | ۲۰ | {۳, ۵} | ۳٫۳٫۳٫۳٫۳ | |
هر جسم افلاطونی با نماد شلفلی {p, q} نشان داده میشود که p تعداد اضلاع (یا رأسهای) هر وجه و q تعداد وجهها (یا اضلاعی) است که در هر رأس به یکدیگر میرسند.
همهٔ اطلاعات ترکیبی این چندوجهیها، شامل تعداد رأسها (V)، اضلاع (E)، و وجهها (F) با استفاده از p و q قابل تعیین هستند. از آنجا که هر ضلع، دو رأس را به یکدیگر متصل کرده و دو وجه مجاور دارد، رابطهٔ زیر برقرار است:
رابطهٔ دیگر بین این مقادیر، با استفاده از مشخصه اولر بدست میآید:
ویژگیهای هندسی[ویرایش]
زاویهها[ویرایش]
زاویه دوسطحی، زاویه داخلی بین هر دو وجه چندوجهی است. اندازهٔ زاویه دوسطحی، θ، برای چندوجهی {p,q} با استفاده فرمول زیر بدست میآید:
کاستی زاویهای هر رأس یک چندوجهی، اختلاف بین مجموع زوایای بین وجهها در هر رأس و ۲π است. کاستی زاویهای، δ، در هر رأس جسم افلاطونی {p,q}، با استفاده از رابطهٔ زیر بدست میآید:
با استفاده از تئوری دکارت، این مقدار برابر است با ۴π تقسیم بر تعداد رأسها (مجموع کاستیها در همهٔ رأسها ۴π است).
معادل ۳-بعدی زاویه سطحی، زاویه فضایی است. زاویه فضایی، Ω، در رأس یک جسم افلاطونی، بر حسب زاویه دوسطحی، بهصورت زیر بدست میآید:
زاویههای مربوط به اجسام افلاطونی در جدول زیر ارائه شدهاند. مقدار زوایای فضایی بر حسب استرادیان داده شده است. ثابت φ = (۱+√۵)/۲، نسبت طلایی است.
| Polyhedron | زاویه دوسطحی | 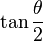 | زاویه رأس | کاستی زاویهای ( ) ) | زاویه فضایی رأس ( ) ) | زاویه فضایی وجه | |
|---|---|---|---|---|---|---|---|
| چهاروجهی | ۷۰٫۵۳° |  | ۶۰° |  |  | 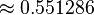 |  |
| مکعب | ۹۰° |  | 90° |  |  | 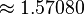 |  |
| هشتوجهی | ۱۰۹٫۴۷° |  | 60°, ۹۰° | 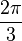 | 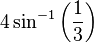 |  |  |
| دوازدهوجهی | ۱۱۶٫۵۷° |  | 108° | 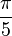 | 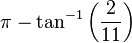 | 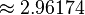 | 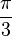 |
| بیستوجهی | ۱۳۸٫۱۹° | 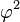 | 60°, ۱۰۸° | 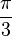 |  | 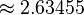 | 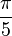 |
شعاعها، مساحت و حجم[ویرایش]
همهٔ اجسام افلاطونی، سه کره هممرکز دارند:
- کرهٔ محیطی که از همهٔ رأسها عبور میکند،
- کرهٔ میانی که بر همهٔ اضلاع در نقطهٔ وسط ضلع مماس است،
- کره محاطی که بر همه وجهها در مرکز وجه مماس است.
شعاع این کرهها، شعاع محیطی، شعاع میانی و شعاع داخلی نامیده میشوند که بهترتیب برابر با فاصله مرکز چندوجهی از رأسها، نقطه وسط اضلاع و مرکز وجهها هستند. شعاع محیطی R و شعاع داخلی r برای چندوجهی {p, q} با طول ضلع a از رابطهٔ زیر بدست میآید:
که θ، زاویه دوسطحی است.
مساحت سطح، A، برای یک جسم افلاطونی {p, q} به آسانی و با استفاده از ضرب تعداد وجهها، F، در مساحت p-ضلعی منتظم بدست میآید: شعاع میانی ρ با استفاده از رابطهٔ زیر بدست میآید:
حجم اجسام افلاطونی برابر است با حاصلضرب F در حجم هرمی با قاعده p-ضلعی منتظم و ارتفاع شعاع داخلی r:
جدول زیر، شعاعها، مساحت و حجم اجسام افلاطونی را ارائه کرده است. در این جدول، طول ضلع a، ۲ در نظر گرفته شدهاست.
| Polyhedron (a = 2) | شعاع داخلی (r) | شعاع میانی (ρ) | شعاع محیطی (R) | مساحت سطح (A) | حجم (V) |
|---|---|---|---|---|---|
| چهاروجهی | 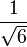 |  | 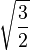 |  |  |
| مکعب |  |  | 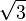 | 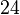 | 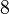 |
| هشتوجهی | 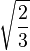 |  |  | 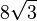 |  |
| دوازدهوجهی |  | 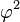 | 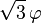 | 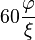 | 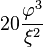 |
| بیستوجهی | 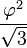 |  |  | 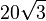 | 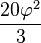 |
ثوابت φ و ξ در جدول بالا عبارتند از: